Здравствуйте друзья, коллеги и все те кто не равнодушен к математике.
Вчера мне удалось доказать Великую теорему Ферма алгебраически частный случай Великой теоремы Ферма алгебраически для таких, x, y, z что x2 + y2 = z2.
Сегодня мне пришла идея доказать её ещё и геометрически и я думаю у меня это получилось.
Сразу хочется отметить, что это тупиковая ветка - которая не имеет дальнейшего развития и приведена здесь исключительно с целью уберечь Вас от этих "граблей". Тупиковой она является, потому что остаётся неопределённость справедливости теоремы для случаев, когда x2 + y2 ≠ z2. То есть не исключена ситуация, когда xn + yn = zn, но при этом x2 + y2 ≠ z2. Например для случаев, когда x + y > z. Тем не менее данное доказательство уже может исключить все варианты для x + y <= z, и предоставить читателям доказать теорему для всех случаев, когда x + y > z.
Данное доказательство - всего лишь творчество автора, не боле того.
Теорема
Для любого натурального числа n > 2 уравнение
xn + xy = zn
не имеет решений в целых числах x > 0, y > 0, z > 0.
Доказательство
Теорема
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:
x2 + y2 = z2.
Доказательство
Возьмём 4 одинаковых прямоугольных треугольника и разместим их в квадрате, как показано на Рис 1.

Рис 1
Их гипотенузы, образуют квадрат см. Рис.2.

Рис 2
Площадь этого квадрата равна: z2.
Теперь переместим треугольники как показано на Рис 3.

Рис 3
После этих преобразований, площадь заштрихованной области, оказалась той же, что и была до преобразования и равна: z2, однако теперь её можно представить как сумму двух квадратов как показано на Рис 4:
- Первый со стороной равной x
- Второй со стороной равной y

Рис 4
Итак теорема доказана: x2 + y2 = z2.
Теперь докажем теорему Ферма для частного случая зафиксировав n = 3 и x2 + y2 = z2.
Формулировка будет звучать следующим образом.
Теорема
Для натурального числа n = 3 уравнение
xn + yn = zn
не имеет решений для целых x > 0, y > 0, z > 0 таких, что x2 + y2 = z2.
Доказательство
Итак, исходя из
теоремы Пифагора, площадь квадрата со стороной равной длине гипотенузы равна сумме площадей со сторонами равными длинам катетов соответственно.
Верно то, что сумма объёмов параллелепипедов полученных из квадратов катетов будет равна объёму куба гипотенузы как показано на Рис.5.
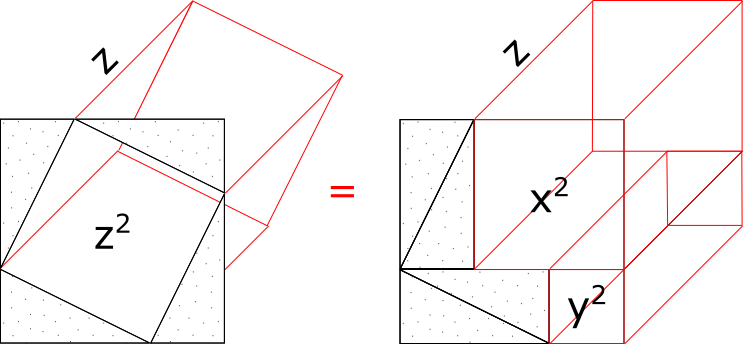
Рис 5
Это верно сходя из:
- Определения объёма как величины равной произведению площади сечения на высоту: v = s * h
- Того факта что сумма площадей катетов равна площади гипотенузы: s = x2 + y2 = z2
- Высоты параллелепипедов полученных из квадратов катетов и высота куба гипотенузы равны, мы взяли их равными длине гипотенузы: h = z
h * (x2 + y2) = h * z2
Заменив x2 + y2 на z2 (по теореме Пифагора) получим:
h * z2 = h * z2.
Поэтому можно точно утверждать, что если величины высот hx = x, hy = y кубов обеих катетов одновременно меньше высоты h = z куба гипотенузы, то сумма объёмов кубов катетов будет так же меньше объёма куба гипотенузы как показано на Рис 6.
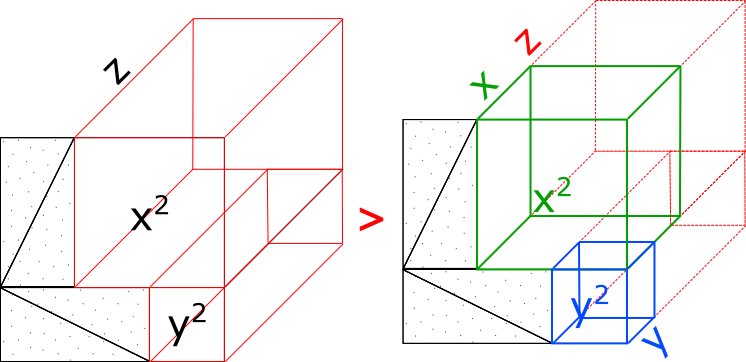
Рис 6
Очевидно, что для всех остальных измерений n > 2 при
x2 + y2 = z2 тенденция сохранится и теорема Ферма для них так же справедлива.
Так же очевидно, что
теорема Ферма справедлива
для всех остальных n > 2 и при x + y < z. Если x + y < z, то
lim (zn - (xn + yn)) → 8.
n → 8
И поскольку начиная с n = 3, объём куба гипотенузы уже больше суммы объёмов кубов катетов, то с увеличением n будет и увеличиваться разница между объёмом куба и суммой объёмов кубов катетов, так никогда и не позволив сравняться им сравняться.
Ссылки
На этом всё, хорошей Вам жизни.
И до новых встреч.